Elliptic Curve And It's Applications

• Introduction
• What is Elliptic Curve
  • The Group Law
• Elliptic Curve's Applications
  • What is discrete logarithm problem
  • ECDSA
  • Diffie-Hellman Key Exchange
  • Schnorr protocol
• Short Weierstrass curves and their representations for fast computations

Introduction

Elliptic curves are a fascinating area of mathematics with profound implications in number theory and cryptography. They provide a rich structure that can be utilized in various applications, particularly in secure communication protocols. In this article, we will explore the fundamental properties of elliptic curves, their group law, and how these mathematical concepts form the basis for several cryptographic algorithms. By understanding elliptic curves, we can gain insight into the underlying principles that ensure the security and efficiency of modern cryptographic systems.

What is Elliptic Curve

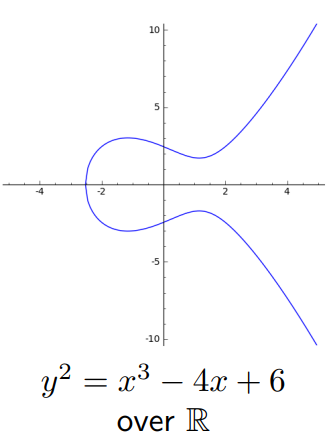
An elliptic curve is the graph of an short Weierstrass equation
$$y^2=x^3+Ax+B$$
where $A$ and $B$ are constants. Below is an example of such a curve.

The Group Law

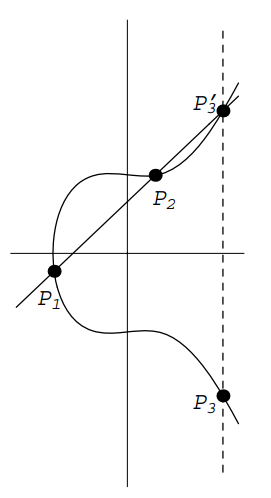
• Adding Points on an Elliptic Curve
  Start with two points
  $$P_1=(x_1,y_1),P_2=(x_2,y_2)$$
  on an elliptic curve $E$ given by the equation $y^2=x^3+Ax+B$. Define a new point $P_3$ as follows. Draw the line $L$ through $P_1$ and $P_2$. We'll see below that $L$ intersects $E$ in a third point $P_3^{\prime }$. Reflect $P_3^{\prime }$ across the $x-$axis (i.e., change the sign of the $y$-coordinate) to obtain $P_3$. We define
  $$P_1+P_2=P_3$$
  Examples below will show that shis is not the same as adding coordinates of the points. It might be better to denote this operation by $P_1+P_2$, but we opt for the simpler notation since we will never be adding points by adding coordinates.
  Assume first that $P_1\ne P_2$ and that neither point is $\infty$. Draw the line $L$ through $P_1$ and $P_2$. Its slope is
  $$m=\frac{y_2-y_1}{x_2-x_1}.$$
  If $x_1=x_2$, then $L$ is vertical. We'll treat this case later, so let's assume that $x_1\ne x_2$. The equation of $L$ is then
  $$y=m(x-x_1)+y_1.$$
  To find the intersection with $E$, substitute to get
  $$(m(x-x_1)+y_1{)}^2=x^3+Ax+B.$$
  This can be rearranged to the form
  $$0=x^3-m^2{x}^2+\dots .$$
  The three roots of this cubic correspond to the three points of intersection of $L$ with $E$. Generally, solving a cubic is not easy, but in the present case we already know two of the roots, namely $x_1$ and $x_2$, since $P_1$ and $P_2$ are points on both $L$ and $E$. Therefore, we could factor the cubic to obtain the third value of x. But there is an easier way. If we have a cubic polynomial $x^3+a{x}^2+bx+c$ with roots $r,s,t$, then
  $$x^3+a{x}^2+bx+c=(x-r)(x-s)(x-t)=x^3-(r+s+t)x^2+\dots .$$ Therefore,
  $$r+s+t=-a.$$
  If we know two roots $r,s$, then we can recover the third as $t=-a-r-s$.
  In our case, we obtain
  $$x=m^2-x_1-x_2$$
  and
  $$y=m(x-x_1)+y_1.$$
  Now, reflect across the $x-$axis to obtain the point $P_3=x_3,y_3$:
  $$x_3=m^2-x_1-x_2,y_3=m(x_1-x_3)-y_1.$$
  In the case that $x_1=x_2$ but $y_1\ne y_2$, the line through $P_1$ and $P_2$ is a vertical line, which therefore intersects E in $\infty$. REflecting $\infty$ across the $x-$axis yields the same point $\infty$(this is why we put $\infty$ at both the top and the bottom of the $y-$axis).Therefore, in this case $P_1+P_2=\infty$.
  Now consider the case where $P_1=P_2=(x_1,y_1).$ When two points on a curve are very close to each other, the line through them approximates a tangent line. Therefore, when the two points coincide, we take the line $L$ through them to be the tangent line. Implicit differentiation allows us to find the slope $m$ of $L$:
  $$2y\frac{dy}{dx}=3x^2+A,\text{ so }m=\frac{dy}{dx}=\frac{3x_1^2+A}{2y_1}.$$
  If $y_1=0$ then the line is vertical and we set $P_1+P_2=\infty$, as before. Therefore, assume that $y_1\ne 0$. The equation of $L$ is
  $$y=m(x-x_1)+y_1,$$
  as before. We obtain the cubic equation
  $$0=x^3-m^2{x}^2+\dots .$$ This time, we know only one root, namely $x_1$, but it is a double root since $L$ is tangent to $E$ at $P_1$. Therefore, proceeding as before, we obtain
  $$x_3=m^2-2x_1,y_3=m(x_1-x_3)-y_1.$$
  Finally, suppose $P_2=\infty$. The line through $P_1$ and $\infty$ is a vertical line that intersects $E$ in the point $P_1^{\prime }$ that is the reflection of $P_1$ across the $x-$axis. When we reflect $P_1^{\prime }$ across the $x-$axis to get $P_3=P_1+P_2$, we are back at $P_1$. Therefore
  $$P_1+\infty =P_1$$
  for all points $P_1$ on $E$. Of course, we extend this to include $\infty +\infty =\infty$.
  Let's summarize the above discussion:

Let $E$ be an elliptic curve defined by $y^2=x^3+Ax+B$. let $P_1=(x_1,y_1)$ and $P_2=(x_2,y_2)$ be points on $E$ with $P_1,P_2\ne \infty$. Define $P_1+P_2=P_3=(x_3,y_3)$ as follows:

• If $x_1\ne x_2$, then $x_3=m^2-x_1-x_2,y_3=m(x_1-x_3)-y_1,$ where $m=\frac{y_2-y_1}{x_2-x_1}$.
• If $x_1=x_2$ but $y_1\ne y_2$, then $P_1+P_2=\infty$.
• If $P_1=P_2$ and $y_1\ne 0$, then $x_3=m^2-2x_1,y_3=m(x_1-x_3)-y_1$, where $m=\frac{3x_1^2+A}{2y_1}$.
• If $P_1=P_2$ and $y_1=0$, then $P_1+P_2=\infty$.
  Moreover, define
  $$P+\infty =P$$
  for all points $P$ on $E$.

The addition of points on an elliptic curve $E$ satisfies the following properties:

• (Commutativity) $P_1+P_2=P_2+P_1$ for all $P_1,P_2$ on $E$.
• (existence of identity) $P+\infty =P$ for all points $P$ on $E$.
• (existence of inverses) Given $P$ on $E$, there exists $P^{\prime }$ on $E$ with $P+P^{\prime }=\infty$. This point $P^{\prime }$ will usually be denoted $-P$.
• (associativity) $(P_1+P_2)+P_3=P_1+(P_2+P_3)$ for all $P_1,P_2,P_3$ on $E$. In other words, the points on $E$ form an additive abelian group with $\infty$ as the identity element.

In cryptography, work over ${\mathbb{F}}_p$ instead of $\mathbb{R}$. We writh group operation additively $(\mathbb{G},+)$. Fix a generator $G\in \mathbb{G}$ of primer order $q$. In practice, $(\mathbb{G},G)$ chosen from some standard(e.g. NIST).

Elliptic Curve's Applications

What is discrete logarithm problem

screct $x\underset{R}{\leftarrow }{\mathbb{F}}_q$, public $xG\in \mathbb{G}$, recovering $x$ from $xG$ is hard.

ECDSA

Elliptic Curve Digital Signature Algorithm

Diffie-Hellman Key Exchange

Diffie-Hellman Key Exchange

Schnorr protocol

$P$ wants to convince $V$ that $P$ knows a secret $s\in {\mathbb{F}}_q$ s.t. $X=sG\in \mathbb{G}$.

Schnorr protocol

Short Weierstrass curves and their representations for fast computations

http://www.hyperelliptic.org/EFD/g1p/auto-shortw.html